合成数据：它是什么以及如何使用它

在现代数据科学和机器学习的领域中，数据是开发预测模型和进行精确分析的基础资源。然而，真实的数据集并非总是可访问、完整或可用的。数据稀缺、固有偏见或隐私限制等问题常常导致获取高质量数据变得困难。这时，“合成数据”的概念应运而生：为了模拟真实数据的特征，同时保护隐私和灵活性而生成的人工数据。

本指南旨在概述生成可靠且实用的合成数据的技术。其中包括探索概率方法、传统机器学习(ML)技术以及大型语言模型(LLM)等高级模型的使用。本指南将提供具体的使用示例，以创建用于训练预测模型和其他分析的实用数据集，确保它们符合现实世界数据的典型约束和特征。

一 什么是合成数据

合成数据是人工生成的信息，模仿真实数据的特征。与直接从观察、实验或传感器收集的数据不同，合成数据是通过算法、数学模型或高级机器学习技术生成的。其主要目的是重现真实数据集中存在的统计结构和关系，即使它们是完全虚构的。

在许多应用领域，收集的数据可能不足以构建稳健的模型。这个问题在观测数据有限的专业领域或工业物联网 (IoT) 应用等新兴领域尤为明显。生成合成数据可以扩展这些数据集，同时保留其基本的统计和结构属性。

这些数据并非简单的匿名或修改过的现有数据副本，而是可以代表原始数据集中未必出现的假设情景或变量的新组合。例如，生成合成图像来训练视觉识别模型，或生成表格数据来模拟经济趋势。

1.合成数据的发展历程

创建合成数据的实践可以追溯到 20 世纪七八十年代，当时计算机模拟开始在科学和工程领域获得广泛关注。当时，蒙特卡罗采样等技术已经被用来基于数学分布生成数据。

21 世纪初，随着隐私保护意识的增强以及真实数据共享法律限制的不断增加，医疗、金融和公共服务等领域涌现出大量合成数据。近年来，机器学习的出现深刻地改变了这一格局。大型语言模型 (LLM) 等先进方法能够创建高度逼真、关系复杂细致的数据。

2.使用合成数据的优点和缺点

以下列出了一些可能让您考虑使用合成数据生成方法的原因。

（1）完全控制：由于数据是人工生成的，因此可以精确地建模其特征，例如分布、相关性和异常值。

（2）可扩展性：一旦设计了合成数据生成器，就可以创建任意大小的数据集，以满足特定的计算或分析需求。

（3）减少偏差：如果设计正确，合成数据可以避免现实世界数据中常见的固有偏差。这使得模型测试能够在更中性和可控的条件下进行。

（4）降低成本：生成合成数据通常比收集真实数据更便宜，特别是在需要复杂设备或大量资源进行获取的领域。

（5）保护隐私：真实数据通常包含敏感信息，这些信息一旦共享，就会面临隐私泄露的风险。由于这些数据并非与真实个人绑定，因此我们可以规避这一问题，同时仍保持分析效用。

（6）克服数据稀缺：收集足够的数据成本高昂或不切实际，例如用罕见疾病的图像训练计算机视觉模型。合成数据可以在不增加额外成本的情况下扩展数据集。

（7）促进实验和开发：合成数据为测试算法和模型提供了一个安全的环境，而不会存在暴露敏感数据或影响真实系统的风险。

（8）创建自定义场景：在某些应用中，需要模拟现实世界中难以观察到的极端事件或不太可能发生的场景。合成数据允许以可控的方式构建这些情况。

尽管合成数据具有诸多优点，但其使用也带来了一些挑战：

（1）合成数据的有效性：合成数据集的质量取决于生成模型捕捉目标领域特征的能力。如果设计不当，合成数据可能会引入错误或扭曲的表征。

（2）法规的接受：在某些领域，合成数据的使用可能尚未被完全接受或监管，这可能会限制其在官方环境中的使用。

（3）维持复杂的关系：重现变量之间的复杂关系（例如在生物或金融系统中观察到的关系）可能特别困难。

（4）合成偏差：虽然合成数据可以减少真实数据中存在的偏差，但如果生成模型基于错误的假设，则存在引入人为偏差的风险。

因此，选择适当的技术并仔细验证结果以确保这些数据在特定应用环境中有用且可靠至关重要。

三 合成数据生成技术

使用概率技术生成合成数据是基于使用数学分布来模拟在真实数据集中观察到的变异性。这种方法允许您建模和创建遵循特定统计分布（例如正态分布、均匀分布或二项分布）的数据。这些方法尤其适用于：

•在受控条件下测试算法。

•为真实数据有限或不可用的情况生成数据集。

•根据定义的概率模型模拟变量之间的关系。

1.基本分布

数学分布，例如正态分布（高斯分布）、均匀分布和泊松分布，是生成合成数据的基本工具。使用 NumPy 等 Python 库，您可以创建代表特定场景的模拟数据集。

示例：生成具有正态分布的数据集

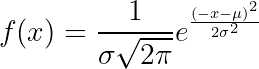
import numpy as np 
import matplotlib.pyplot as plt 

# 生成正态分布数据
mu, sigma = 0, 1 # 平均值和标准差
data_normal = np.random.normal(mu, sigma, 1000) 

# 可视化
plt.hist(data_normal, bins=30, alpha=0.7, color='blue', edgecolor='black') 
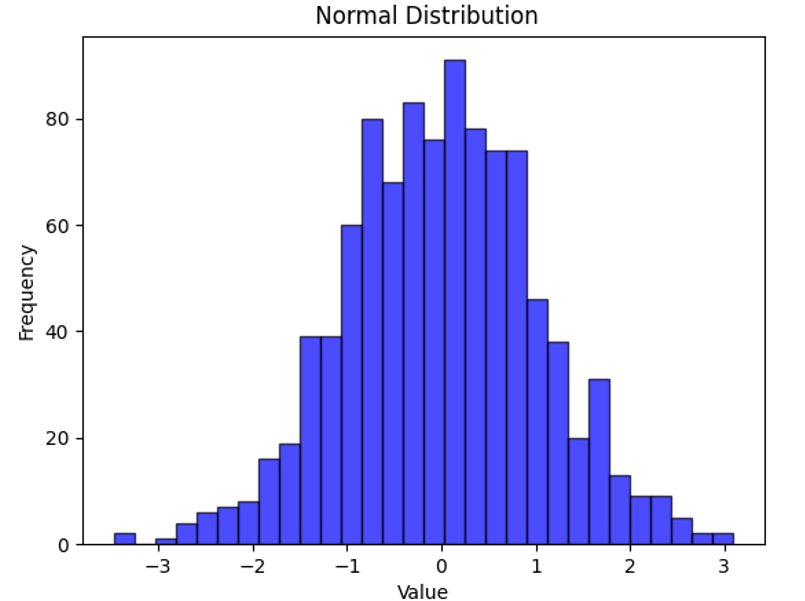
plt.title('正态分布') 
plt.xlabel('值') 
plt.ylabel('频率') 
plt.show()
 

2.蒙特卡罗采样

蒙特卡洛采样是一种通过模拟更复杂的分布或由任意复杂函数定义的分布来生成数据的技术。当简单分布无法满足需求时，它是理想的选择。

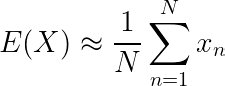
示例：使用蒙特卡洛近似积分。

import numpy as np 
import matplotlib.pyplot as plt 

# 真实分布的参数（等待时间）
real_mu = 10 # 平均值
real_sigma = 2 # 标准差
n_real_samples = 10000 # 真实数据数量（样本）

# 真实数据生成（观测分布）
real_data = np.random.normal(real_mu, real_sigma, n_real_samples) 

# 蒙特卡洛：用于近似真实分布的渐进样本
n_monte_carlo_samples = 500 # 蒙特卡洛样本的最大数量
monte_carlo_data = np.random.normal(real_mu, real_sigma, n_monte_carlo_samples) 

# 创建图表来比较真实分布和蒙特卡洛模拟
plt.figure(figsize=(12, 6)) 

# 真实分布
plt.hist(real_data, bins=30, alpha=0.5, color='blue', label='真实分布', density=True) 

# 蒙特卡洛分布
plt.hist(monte_carlo_data, bins=30, alpha=0.5, color='orange', label='蒙特卡洛', density=True) 

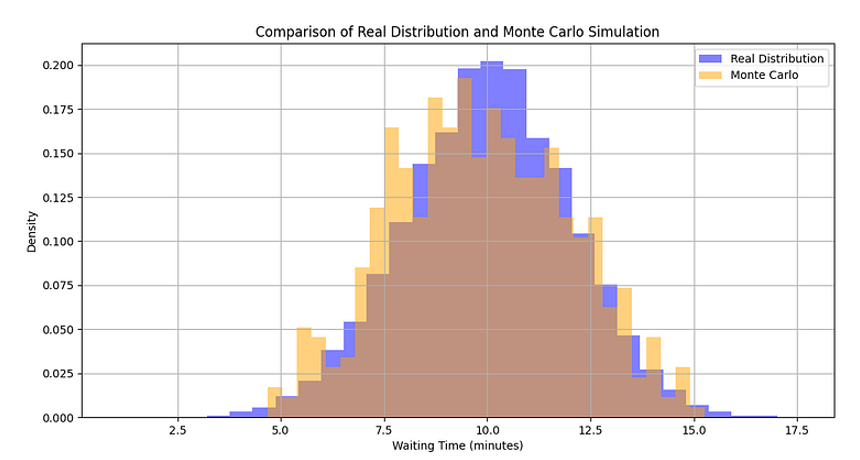
plt.title("真实分布与蒙特卡洛模拟的比较") 
plt.xlabel("等待时间（分钟）") 
plt.ylabel("密度") 
plt.legend() 
plt.grid(True) 
plt.show()

3.条件分布

条件分布允许你模拟变量之间存在相关性的数据集。这对于生成维持数据集维度之间有意义关系的合成数据至关重要。

示例：多元正态分布

mean = [0, 0] # X 和 Y 的平均值
covariance = [[1, 0.8], [0.8, 1]] # 协方差矩阵
data_multivariate = np.random.multivariate_normal(mean, covariance, 500) 

# 可视化
plt.scatter(data_multivariate[:, 0], data_multivariate[:, 1], alpha=0.6) 
plt.title('多元正态分布') 
plt.xlabel('X') 
plt.ylabel('Y') 
plt.axis('equal') 
plt.show()

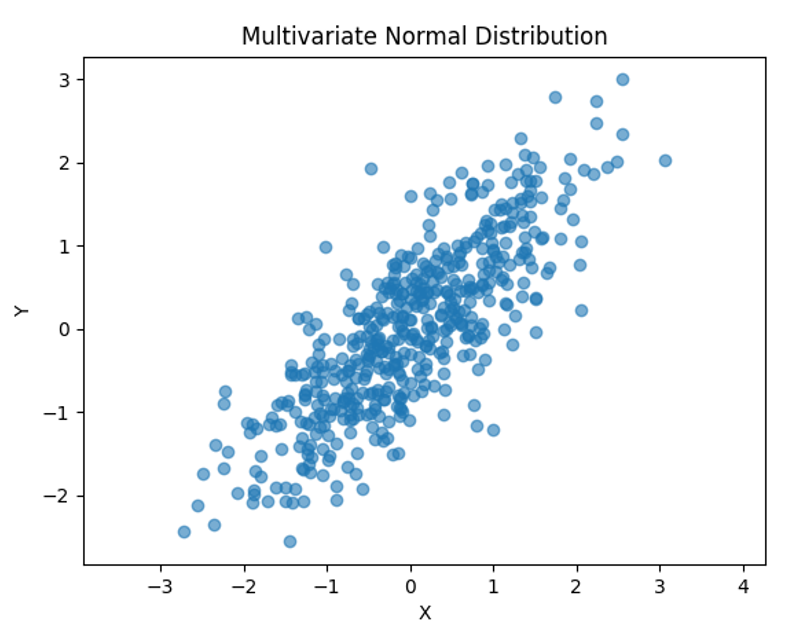
基于统计分布的数据生成方法具有诸多优势。它们允许完全控制，能够定义特定参数，确保数据按照定义明确的统计模型生成。此外，它们还具有灵活性，能够轻松适应不同情况，例如需要单峰或多峰分布的情况。从操作角度来看，它们被证明特别高效，因为即使对于大型数据集，数据生成也快速且充分。

然而，它们也存在一些局限性。这些方法最适用于统计结构简单清晰的数据集，但在表示复杂或非线性关系方面效果较差。此外，为了获得有用的结果，必须深入了解分布及其参数，这要求使用方法的人具备一定的技术专业知识。

完整示例：具有特定关系的数据生成

让我们创建一个合成数据集，其中包含两个变量之间的噪声线性关系，例如身高和体重。

# 参数
np.random.seed(42) 
n_samples = 1000 
slope = 2.5 # 线性关系的斜率
intercept = 50 # 截距
noise_level = 5 # 噪声水平

# 数据生成
heights = np.random.normal(170, 10, n_samples) # 正态分布的身高
weights = slope * heights + intercept + np.random.normal(0, noise_level, n_samples) 

# 可视化
plt.scatter(heights, weights, alpha=0.6) 
plt.title('综合线性关系 (身高 vs 体重)') 
plt.xlabel('身高 (cm)') 
plt.ylabel('体重 (kg)') 
plt.show()

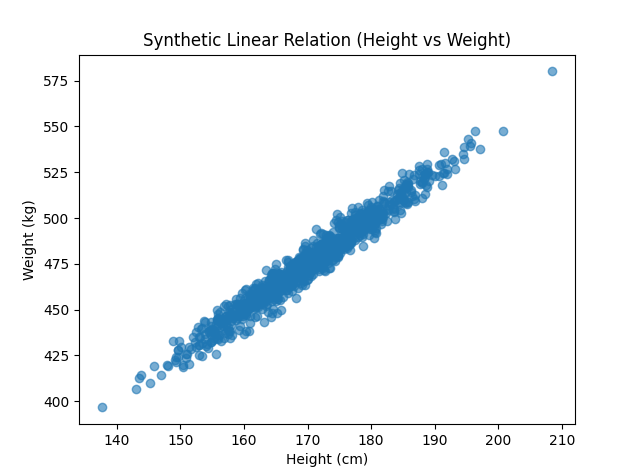
4.使用传统机器学习方法生成数据

使用传统机器学习方法生成合成数据是一种广泛使用的技术，用于扩展现有数据集或创建新数据集，同时保持合理的结构和分布。与深度神经网络等高级方法不同，这些方法易于实现，并且可以直接控制生成数据的特征。

（1）高斯混合模型

高斯混合模型 (GMM) 是一种概率模型，它将数据集表示为多个高斯分布的组合。GMM 中的每个聚类都对应一个高斯分量。这种方法对于生成模拟多类数据集的数据特别有用。

示例：使用 GMM 根据样本数据生成合成数据集

import numpy as np 
import matplotlib.pyplot as plt 
from sklearn.mixture import GaussianMixture 

# 原始数据：两个主要聚类
np.random.seed(42) 
data_original = np.concatenate([ 
    np.random.normal(loc=0, scale=1, size=(100, 2)), 
    np.random.normal(loc=5, scale=1.5, size=(100, 2)) 
]) 

# 创建 GMM 模型
gmm = GaussianMixture(n_components=2, random_state=42) 
gmm.fit(data_original) 

# 生成新的合成数据
data_sintetici = gmm.sample(200)[0] 

# 并排可视化
fig, axes = plt.subplots(1, 2, figsize=(12, 6), sharex=True, sharey=True) 

# 原始数据图
axes[0].scatter(data_original[:, 0], data_original[:, 1], alpha=0.6, label="Original Data") 
axes[0].legend() 
axes[0].set_title("Original Data") 
axes[0].grid(True) 

# 合成数据图
axes[1].scatter(data_sintetici[:, 0], data_sintetici[:, 1], color='r', alpha=0.6, label="Dati Sintetici") 
axes[1].legend() 
axes[1].set_title("Synthetic Data Generated with GMM") 
axes[1].grid(True) 

plt.tight_layout() 
plt.show()

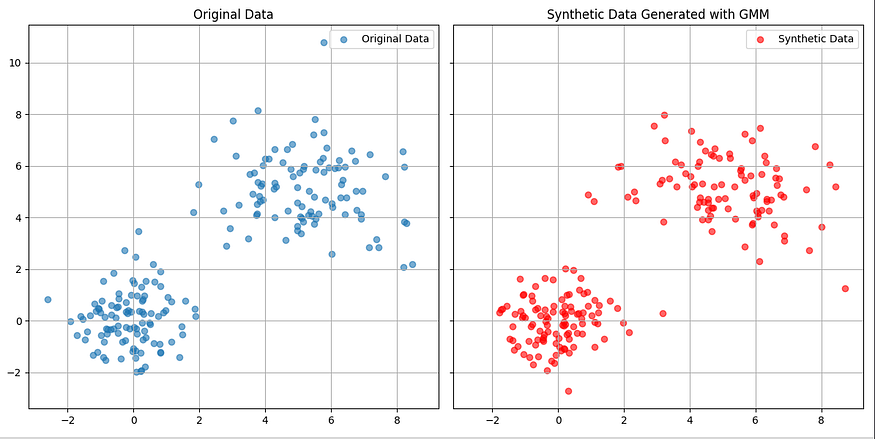
这种方法的主要优点之一是能够直接控制聚类数量和方差，从而实现更有针对性和个性化的分析。此外，它对于具有多峰分布的数据特别有效，能够很好地近似其结构。

然而，该方法也存在一些局限性。该方法仅适用于能够用高斯分布建模的数据集，这限制了其应用范围。此外，它需要预先确定最佳组件数量，这在更复杂的环境中可能是一个挑战。

（2）生成决策树

生成决策树在变量之间建立条件关系。它们可用于生成遵循复杂模式的数据，例如逻辑约束或变量之间的依赖关系。

示例：根据条件规则生成合成数据集。

import numpy as np 
import matplotlib.pyplot as plt 
from sklearn.mixture import GaussianMixture 
from sklearn.tree import DecisionTreeClassifier 
import pandas as pd 

# 创建一个简单的数据集
np.random.seed(42) 
data_original = pd.DataFrame({ 
    'Feature1': np.random.choice([0, 1], size=100), 
    'Feature2': np.random.choice([0, 1], size=100), 
    'Label': np.random.choice([0, 1], size=100) 
}) 

# 构建决策树
X = data_original[['Feature1', 'Feature2']] 
y = data_original['Label'] 
tree = DecisionTreeClassifier(max_depth=3, random_state=42) 
tree.fit(X, y) 

# 生成新数据
syntetic_data = pd.DataFrame({ 
    'Feature1': np.random.choice([0, 1], size=100), 
    'Feature2': np.random.choice([0, 1], size=100) 
}) 
synthesized_data['Label'] = tree.predict(synthetic_data) 

print("生成的合成数据:\n", synthesized_data.head())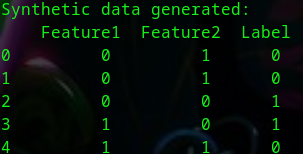

这种方法的主要优点之一是其灵活性，甚至可以对复杂的规则进行建模。当您想要复制变量之间存在条件关系的数据集时，这种方法尤其有用，可以确保数据结构的一致性。

然而，该方法也存在一些局限性。它可能会导致原始数据过度拟合，从而降低其泛化能力。此外，它并非生成高变异性数据集的最佳解决方案，因为在高变异性数据集中，保持数据的代表性更加困难。

5.使用 LLM（大型语言模型）生成合成数据

大型语言模型 (LLM) 代表了生成合成数据的最先进技术之一。它们将自然语言理解和生成功能与深度学习的强大功能相结合，使其成为创建结构化、连贯且个性化数据集的理想工具。在本节中，我们将探索如何使用 LLM 生成合成数据，并通过实际示例和 Python 代码来演示其应用。

像 GPT 或 BERT 这样的 LLM 可以通过训练或调整来创建合成数据，这得益于它们具有以下能力：

•理解背景：他们可以分析和生成具有复杂关系的数据，以适应特定的背景。

•个性化：它们提供生成符合用户定义的规则或模式的数据的能力。

•对非结构化数据的有效性：它们对于生成文本和表格数据特别强大。

示例：创建表格数据集

让我们考虑这样一种情况：我们想要为营销应用程序生成一个表格数据集，其中包含客户信息，例如年龄、城市和年收入。

步骤 1：定义提示

有效的提示能够引导大型语言模型 (LLM) 撰写连贯的数据。以下是示例提示：

生成一个包含 10 行 4 列的数据集：\n“ 
Job”（表示人员职业的字符串）、“ 
Age”（18 到 75 之间的整数）、“ 
Country”（表示国家名称的字符串）
和“Score”（0 到 100 之间的浮点数）。\n\n“ 
“Job | Age | Country | Score\n” 


“---------------------------------\n” 
“Teacher | 30 | USA | 88.5\n” 
“Engineer | 45 | UK | 92.3\n” 
“Nurse | 28 | Canada | 75.4\n” 
“Artist | 33 | France | 68.9\n” 
“Doctor | 50 | Germany | 85.1\n”

步骤2：使用Python生成数据

借助“transformers”之类的库，我们可以与预先训练的模型交互来生成数据集：

from transformers import GPTNeoForCausalLM, GPT2Tokenizer 
import torch 
import re 

# 加载 tokenizer 和 hugging face 模型
model_name = "EleutherAI/gpt-neo-1.3B" 
tokenizer = GPT2Tokenizer.from_pretrained(model_name) 
tokenizer.pad_token = tokenizer.eos_token 
model = GPTNeoForCausalLM.from_pretrained(model_name) 
model.config.pad_token_id = tokenizer.eos_token_id 
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") 
model.to(device) 
model.eval() 

prompt = ( 
    "生成一个包含 10 行 4 列的数据集：\n" 
    "Job（表示人员职业的字符串）、" 
    "Age（18 到 75 之间的整数）、" 
    "Country（表示国家名称的字符串）、" 
    "and Score（浮点数）介于 0 和 100 之间）。\n\n" 
    "工作 | 年龄 | 国家 | 年收入\n" 
    "---------------------------------\n" 
    "教师 | 30 | 美国 | 88.5\n" 
    "工程师 | 45 | 英国 | 92.3\n" 
    "护士 | 28 | 加拿大 | 75.4\n" 
    "艺术家 | 33 | 法国 | 68.9\n" 
    "医生 | 50 | 德国 | 85.1\n" 
) 

# 对提示进行编码
inputs = tokenizer(prompt, return_tensors="pt", padding=True).to(device) 
input_ids = inputs['input_ids'] 
attention_mask = inputs['attention_mask'] 

# 生成文本
output = model.generate( 
    input_ids=input_ids, 
    attention_mask=attention_mask, 
    max_length=input_ids.shape[1] + 200, 
    num_return_sequences=1, 
    no_repeat_ngram_size=2, 
    do_sample=False, 
    temperature=0.7, 
    pad_token_id=tokenizer.eos_token_id 
) 

# 解码输出
generated_text = tokenizer.decode(output[0], skip_special_tokens=True) 
print(generated_text) 

# 提取阅读模式
data_pattern = re.compile( 
    r"([A-Za-z\s]+)\s*\|\s*(\d{1,2})\s*\|\s*([A-Za-z\s]+)\s*\|\s*(\d{1,3}\.\d+)" 
) 
matches = data_pattern.findall(generated_text) 

print("\nExtracted Data:") 
for match in matches: 
    print(f"Job: {match[0].strip()}, Age: {match[1]}, 国家: {match[2].strip()}, 收入: {match[3]}")

提取的数据：
工作：教师，年龄：30，国家：美国，收入：88.5
工作：工程师，年龄：45，国家：英国，收入：92.3
工作：护士，年龄：28，国家：加拿大，收入：75.4
工作：艺术家，年龄：33，国家：法国，收入：68.9
工作：医生，年龄：50，国家：德国，收入：85.1
工作：经理，年龄：25，国家：西班牙，收入：77.8
工作：销售员，年龄：35，国家：日本，收入：73.6
工作：司机，年龄：20，国家：澳大利亚，收入：71.2
工作：办事员，年龄：40，国家：印度，收入：70.7
工作：学生，年龄：24，国家：中国，收入：69.0
工作：面包师，年龄：22，国家：巴西，收入：66.75
工作：女佣，年龄： 23，国家：意大利，收入：65.25
职业：厨师，年龄：21，国家：希腊，收入：64.15
职业：家庭主妇，年龄：26，国家：土耳其，收入：63.85
职业：渔夫，年龄：29，国家：俄罗斯，收入：62.65
职业：搬运工，年龄：27，国家：南非，收入：61.45
职业：水手，年龄：32，国家：美国，收入：60.35
职业：士兵，年龄：31，国家：瑞典，收入：59.05
职业：警察，年龄：34，国家：荷兰，收入：58.95
职业：护理人员，年龄：36，国家：比利时，收入：57.55
职业：建筑工人，年龄：37，国家：丹麦，收入：56.40
职业：电工，年龄：38，国家：挪威，收入： 55.10

LLM（大型语言模型）拥有众多优势，使其成为用途极为广泛的工具。首先，它们具有极大的灵活性：能够生成结构化和非结构化数据，从而适应多种需求。此外，通过使用 API 和 Python 库，它们可以简化与工作流程的集成，从而实现快速有效的实施。

另一个积极的方面是定制的可能性：可以轻松修改提示以满足特定需求，从而使这些模型在目标环境中更有用。

然而，需要考虑一些限制和关键方面。例如，生成数据的质量很大程度上取决于所使用的公式和模型的设置。

另一个需要注意的因素是偏差的存在：由于模型是从训练数据中学习的，因此它们可能会重现数据中已经存在的偏差或扭曲。最后，成本也是一个重要因素，尤其是在生产环境中，大量使用LLM可能会导致巨额成本。

6.具有特定结构和关系的数据生成

生成具有特定结构和关系的合成数据是一项高级实践，需要运用技术在遵循复杂约束的同时创建人工数据集。这种方法对于模拟至关重要，因为合成数据必须代表真实场景或补充现有数据集，且不损害其完整性。

在许多情况下，生成具有明确结构的数据都非常有用。例如，在金融模拟中，生成遵循变量间特定相关性的时间序列非常重要。在物理学领域，创建遵循特定方程或自然法则的数据至关重要。然而，在生物信息学中，构建考虑特定研究背景中的生物或化学约束的数据集至关重要。

主要目标是创建不仅具有统计代表性而且符合其所指应用领域的规则和关系特征的合成数据。

（1）处理复杂的关系

示例：固定总和数据生成

一个常见的情况是生成遵守总和约束的变量，例如不同部门之间的预算分配。

import numpy as np 
import pandas as pd 

# 观察值和类别的数量
n_observations = 100 
n_categories = 3 

# 每个观察值的总和
total_sum = 100 

# 生成随机数据
data = np.random.dirichlet(np.ones(n_categories), size=n_observations) * total_sum 

# 创建 DataFrame 
df = pd.DataFrame(data, columns=[f"Category_{i+1}" for i in range(n_categories)]) 
df["Total"] = df.sum(axis=1) 

print("使用固定和生成的数据集示例：") 
print(df.head()) 

>>>

使用固定和生成的数据集示例：
Category_1 Category_2 Category_3 Total 
0 58.673361 34.972747 6.353891 100.0 
1 16.882673 14.145658 68.971669 100.0 
2 71.446625 10.170256 18.383118 100.0 
3 57.066341 37.334702 5.598957 100.0 
4 15.686990 3.622839 80.690171 100.0

狄利克雷分布用于生成随机比例，每个比例代表总数的一部分。这些比例一旦计算出来，就会进行缩放，使其总和等于定义为 total_sum 的特定值。这样，该函数生成的数据就遵循了基本约束，即所有比例的总和恰好等于指定的目标值。

示例：具有预定义相关性的数据

另一个常见的需求是生成具有变量之间特定相关性的合成数据。

from scipy.stats import norm 

# 数据集的维度
n_samples = 1000 

# 所需的相关矩阵
correlation_matrix = np.array([[1.0, 0.8, 0.5], [0.8, 1.0, 0.3],[0.5, 0.3, 1.0]]) 

# 创建相关数据
mean = [0, 0, 0] 
data = np.random.multivariate_normal(mean, correlation_matrix, size=n_samples) 

# 转换为 DataFrame 
df_corr = pd.DataFrame(data, columns=["Variable_1", "Variable_2", "Variable_3"]) 
print(df_corr.corr()) 

>>> 

             Variable_1 Variable_2 Variable_3 
Variable_1 1.000000 0.784861 0.490152 
Variable_2 0.784861 1.000000 0.263210
变量_3 0.490152 0.263210 1.000000

multivariate_normal 函数允许您生成遵循多元分布的数据，尊重作为输入提供的相关矩阵建立的相关性。

（2）基于图的模型

基于图的模型对于模拟社交网络、交易或信息流很有用。

导入 networkx 作为 nx
导入 pandas 作为 pd
导入 matplotlib.pyplot 作为 plt 

# 创建因果图
n_nodes = 10 
p_connection = 0.3 
graph = nx.erdos_renyi_graph(n_nodes, p_connection) 

# 转换为 DataFrame 
edges = nx.to_pandas_edgelist(graph) 
print("连接列表（弧）：") 
print(edges) 

# 图形可视化
plt.figure(figsize=(8, 6)) 
nx.draw(graph, with_labels=True, node_color='lightblue', edge_color='gray', node_size=700, font_size=10) 
plt.title("因果图的表示") 
plt.show()

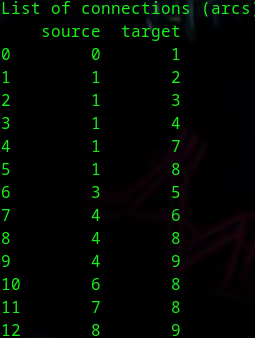
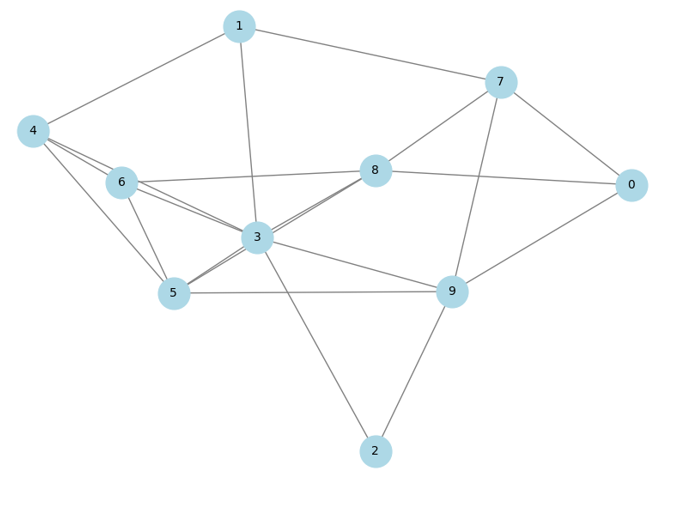
这一背景下的主要应用包括：一方面，社交网络的模拟，它可以分析和预测虚拟或现实社区中的互动动态和集体行为。另一方面，我们发现分布式系统中的数据流建模是理解、优化和管理复杂且互联的技术环境中信息传输的关键活动。

（3）时间序列的自回归模型

自回归时间序列用于模拟具有时间依赖性的数据。

导入 numpy 作为 np
导入 networkx 作为 nx
导入 pandas 作为 pd
导入 matplotlib.pyplot 作为 plt
从 statsmodels.tsa.arima_process 导入 ArmaProcess 

# 定义 AR 和 MA 参数
ar_params = np.array([1, -0.5]) 
ma_params = np.array([1, 0.4]) 
model = ArmaProcess(ar=ar_params, ma=ma_params) 

# 生成时间序列
n_points = 200 
time_series = model.generate_sample(nsample=n_points) 

# 可视化
导入 matplotlib.pyplot 作为 plt 
plt.plot(time_series) 
plt.title("自回归时间序列") 
plt.show()

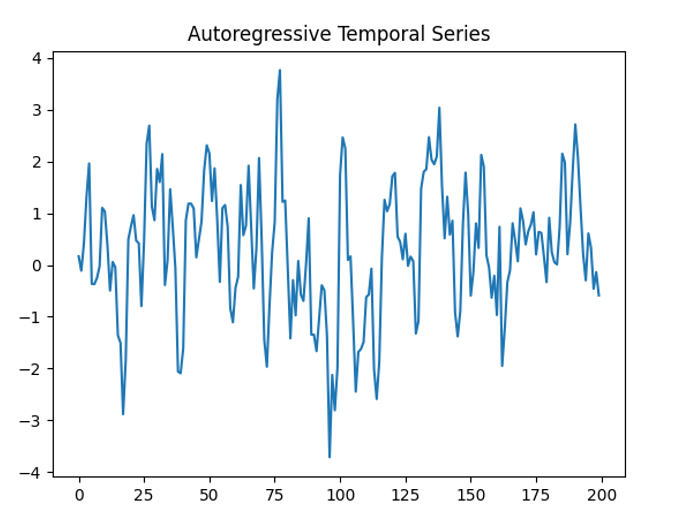
四 合成数据生成中的伦理考虑和限制

合成数据的生成提供了一种创新而灵活的解决方案，可以克服与真实数据的可用性、质量和保护相关的挑战，但它也引发了需要仔细评估的重大道德和操作问题。

一个问题涉及与真实数据过度相似的风险。如果合成数据过于忠实于原始来源，则可能会泄露个人敏感信息。此外，将这些数据与其他数据集相结合，有助于识别其中的关联性，从而促进重新识别。

另一个关键问题是原始数据中存在的偏差可能会被转移或放大。如果在生成过程中没有进行严格的控制，合成数据确实可能会使类别不平衡或属性永久化。此外，在创建过程中，可能会引入新的无意偏差，从而加剧问题。

合成数据的有效性和可用性是另一个挑战。为了发挥作用，数据必须遵循现实世界数据固有的关系和约束，例如求和或时间序列。如果缺少这些特征，合成数据可能无法使用。此外，基于合成数据训练的机器学习模型可能无法充分推广到现实世界。

从监管和道德角度来看，合成数据的生成必须符合数据保护法，例如欧洲的《通用数据保护条例》（GDPR）或美国的《消费者隐私法案》（CCPA）。这意味着对原始数据进行严格管理，并在流程的每个阶段都遵守法律要求。

五 小结

合成数据生成正逐渐成为数据科学和机器学习中的关键要素，尤其是在真实数据可用性受到隐私限制、偏见或缺乏代表性等因素限制的情况下。然而，其有效性取决于选择最合适的技术，并意识到其局限性和伦理影响。

在现有的技术中，概率技术被证明能够简单有效地表示线性分布，尽管它们在处理复杂数据时存在局限性。传统的机器学习方法在简单性和捕捉更复杂结构的能力之间取得了良好的平衡。高级语言模型（例如大型语言模型）以其灵活性而著称，能够生成高度真实且复杂的数据，非常适合模拟、表格分析和文本等应用场景。

为了最大限度地发挥合成数据的价值，至关重要的是要根据具体需求定制生成策略，持续监控所生成数据的质量，并将其与真实数据进行比较。此外，还需要整合控制措施以减轻偏见和隐私侵犯，并及时了解该领域的快速技术发展。

来源（公众号）：数据驱动智能